常见的启发式优化算法

技术
5.7k 词

引子

最近在中科院自动化所实习，其中负责了一个保密项目，项目主要涵盖了多目标优化算法。可能是场景比较复杂，发现使用 scipy.optimize 中的 minimize 方法得出了与实际值（暴力搜索）相差较大的结果。因此，我开始了解到一些启发式优化算法，如模拟退火、粒子群优化、遗传算法等。它们不同于传统的梯度下降法，而是通过模拟自然界中的某些现象来寻找全局最优解。使用了这些方法之后，发现效果与暴力搜索结果相差很小，并且速度有了很大的提升。这里我将介绍一些常见的启发式优化算法（我觉得这些算法非常地形象，很好理解 😃）。


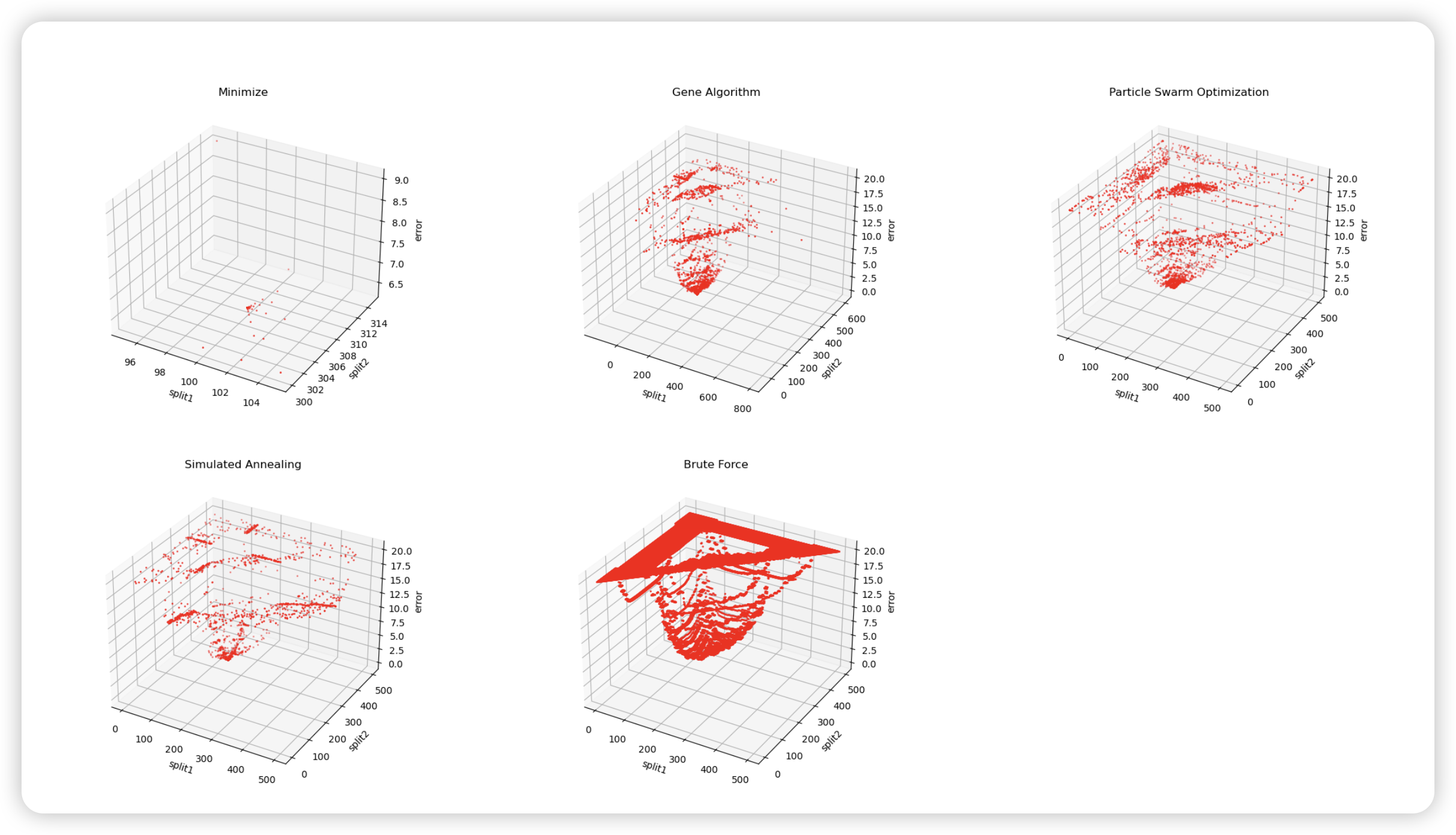
这张图描绘了我的问题中采用多种优化方法的解的情况。（误差上界为 20，超出 20 的都改成了 20 以增强可视化效果）

0x01. 遗传算法 (Genetic Algorithm)

遗传算法，顾名思义，就是模拟生物的遗传过程，它通过模拟自然选择中的优胜劣汰，来寻找优化目标全局最优解。让我们回顾中学时学过的生物课：在自然界中，适应能力高的个体会更容易存活下来，而适应能力低的个体会逐渐消失。种群内的个体在繁殖时，会发生基因重组、基因突变等现象，使得后代的性状发生改变，保持其基因多样性。而遗传算法正是基于这些现象来寻找全局最优解的。

一般来说，遗传算法的步骤有初始化种群、选择、交叉、变异。在初始化了种群之后，就不断地执行之后的步骤，直到满足终止条件。

1. 初始化种群

1
2
3
def init_population(pop_size):
    population = np.random.normal(0, 1, (pop_size, 2)) # 采用正态分布初始化种群，这里假设个体是一个二维向量。
    return population

2. 适应度函数

通过适应度函数来“选择”出适应能力高的个体。适应度函数在优化问题中也可以采用目标函数来代替。

1
2
def fitness_func(population):
    return np.sum(population ** 2, axis=1) # 这里假设目标函数是 f(x) = x1^2 + x2^2。

3. 选择 (Selection)

有了适应性函数，我们就可以确定谁的适应性高，更符合条件了。但是如何从种群中选择出适应性高的个体呢？很容易就可以想到通过“加权”的方式来选择，即适应性强的个体被选择的几率更大，这就是最基本的选择方法：轮盘赌。

轮盘赌中，每个个体被选中的概率为

$ P_i = \frac{f_i}{\sum_{j=1}^{N} f_j} $

其中，$ f_i $ 为个体 $ i $ 的适应度，$ N $ 为种群大小。

1
2
3
4
5
def select(population, fitness):
    prob = fitness / np.sum(fitness)
    idx = np.random.choice(np.arange(len(population)), size=len(population), p=prob)
    # p 为每个个体被选中的概率
    return population[idx]

然而，能够发现，如果个体的适应度差距较大，就可能导致适应度最高的个体反复被选择，而适应度低的可能一直得不到选择，导致解多样性降低，解空间减少，从而过早收敛。在比较复杂的问题下，这种情况可能会导致算法陷入局部最优解。这里就有了第二个方法，也是当今遗传算法中最常用的方法：锦标赛选择。

竞标赛选择法随机选择 $ k $ 个个体，然后从中选择适应度最高的个体。这个过程重复 $ N $ 次，直到选择出 $ N $ 个个体。

1
2
3
4
5
6
def tournament_select(population, fitness, k=2, N=10):
    selected = []
    for _ in range(N):
        idx = np.random.choice(np.arange(len(population)), size=k)
        selected.append(population[np.argmax(fitness[idx])])
    return np.array(selected)

此外，还有一些其他的选择方法，如：线性排名选择、指数排名选择等。

4. 交叉 (Crossover)

交叉模拟了生物的基因重组过程。在交叉过程中，两个个体的基因会发生重组，产生新的个体。交叉的方式有很多种，如单点交叉、多点交叉、均匀交叉等。这里我们以单点交叉为例。

单点交叉会随机选择一个交叉点，然后将两个个体的基因在交叉点处进行交换。

1
2
3
4
5
def crossover(parent1, parent2):
    point = np.random.randint(0, len(parent1))
    child1 = np.concatenate([parent1[:point], parent2[point:]])
    child2 = np.concatenate([parent2[:point], parent1[point:]])
    return child1, child2

5. 变异 (Mutation)

变异模拟了生物的基因突变过程。在变异过程中，个体的基因会发生随机变化，引入适当的多样性。变异算子同样有很多种，如：高斯变异、均匀变异等。这里我们以均匀变异为例。

均匀变异会随机选择一个基因，然后将其变异为另一个值。

1
2
3
4
5
def mutation(child, prob=0.1):
    for i in range(len(child)):
        if np.random.rand() < prob:
            child[i] = np.random.normal(0, 1)
    return child

交叉算子因其全局搜索能力而作为主要算子。变异算子通过对个体进行小幅度的随机调整，在当前搜索区域内进行细致的搜索和优化，因其局部搜索能力而作为辅助算子。

遗传算法就是在不断地重复选择、交叉、变异的过程中，逐渐逼近全局最优解。

这是一个非常成熟的算法，也有一些很好的 Python 库可以使用，如 deap。

模拟退火算法 (Simulated Annealing)

模拟退火算法的灵感来源于金属退火过程。在金属加热后的退火过程中，会缓慢冷却达到低能量状态，即高度有序的晶体结构。

具体来说，它需要一个初始温度 $ T $ 和一个降温速率 $ \alpha $。在每一次迭代中，算法会随机从当前解的邻域中选择一个新解，然后计算新解的能量。如果新解的能量比当前解的能量更低，那么就接受新解。如果新解的能量比当前解的能量更高，那么就以一定的概率接受新解。这个概率由下式给出：

$ P = e^{-\frac{E_{new} - E_{old}}{T}} $

其中，$ E_{new} $ 为新解的能量，$ E_{old} $ 为当前解的能量。

这里聚焦的是最小化优化问题，因此能量低的（解更小）被认为是更优的解。不管怎么样，都会有可能接受一个较差解（能量高的），这与传统的贪心算法不同，避免了早期陷入局部最优解的问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 假设目标函数为 f(x) = x1^2 + x2^2
def objective_func(x):
    return np.sum(x ** 2)

def simulated_annealing(T, alpha, max_iter):
    x = np.random.normal(0, 1, 2)
    E = objective_func(x)
    for _ in range(max_iter):
        x_new = x + np.random.normal(0, 1, 2)
        E_new = objective_func(x_new)
        if E_new < E or np.random.rand() < np.exp(-(E_new - E) / T):
            x = x_new
            E = E_new
        T *= alpha
    return x

x = simulated_annealing(100, 0.99, 1000)
print(x)

在我的问题中，对于这三种方法，模拟算法所花费的时间非常少。

scipy 中有模拟退火算法的实现，可以直接使用。

粒子群优化算法 (Particle Swarm Optimization)

粒子群优化算法是一种基于群体智能的优化算法，模仿了鸟群、鱼群等社会动物群体的行为，通过个体间的信息共享实现全局最优解的搜索。

在粒子群优化算法中，每个个体被称为粒子，每个粒子都有自己的位置和速度。粒子的位置代表了解空间中的一个解，而粒子的速度代表了粒子在解空间中的搜索方向。粒子的速度会受到自身的历史最优解和群体的历史最优解（整个群体中目前的最优的解）的影响，根据个体最佳位置和群体最佳位置进行更新，具体的更新公式如下：

速度更新公式：

$ v_{i}^{t+1} = w \cdot v_{i}^{t} + c_1 \cdot r_1 \cdot (pbest_{i} - x_{i}^{t}) + c_2 \cdot r_2 \cdot (gbest - x_{i}^{t}) $

位置更新公式：

$ x_{i}^{t+1} = x_{i}^{t} + v_{i}^{t+1} $

其中，$ v_{i}^{t} $ 为粒子 $ i $ 在第 $ t $ 代的速度，$ x_{i}^{t} $ 为粒子 $ i $ 在第 $ t $ 代的位置，$ pbest_{i} $ 为粒子 $ i $ 的历史最优位置，$ gbest $ 为群体的历史最优位置，$ w $ 为惯性权重，$ c_1 $ 和 $ c_2 $ 为加速因子，控制粒子向个体最佳位置和群体最佳位置的加速程度，$ r_1 $ 和 $ r_2 $ 为随机数。

w 相当于给了粒子记忆历史速度的能力，让历史速度也有一部分权重参与新速度的生成，就如同控制学习率的动量法一样。

我们依旧以目标函数 $ f(x) = x1^2 + x2^2 $ 为例，来实现粒子群优化算法。

1
2
def objective_func(x):
    return np.sum(x ** 2)

一些参数设定：

1
2
3
4
5
6
7
num_particles = 30
dimensions = 2
bounds = [-10, 10] # 解空间的边界
max_iterations = 100
w = 0.5
c1 = 1.5
c2 = 1.5

初始化粒子群：

1
2
3
4
5
# 初始化粒子群
def initialize_particles(num_particles, dimensions, bounds):
    particles = np.random.uniform(bounds[0], bounds[1], (num_particles, dimensions)) # (30, 2)
    velocities = np.random.uniform(-1, 1, (num_particles, dimensions)) # (30, 2)
    return particles, velocities

更新粒子群：

1
2
3
4
5
6
# 更新粒子速度和位置
def update_particles(particles, velocities, p_best, g_best, w, c1, c2):
    r1, r2 = np.random.rand(), np.random.rand()
    velocities = w * velocities + c1 * r1 * (p_best - particles) + c2 * r2 * (g_best - particles)
    particles = particles + velocities
    return particles, velocities

主算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# PSO算法
def pso(num_particles, dimensions, bounds, max_iterations, w, c1, c2):
    particles, velocities = initialize_particles(num_particles, dimensions, bounds)
    p_best = particles.copy()
    p_best_scores = np.apply_along_axis(objective_function, 1, p_best) # 每个粒子历史最优解 (30,)
    g_best = particles[np.argmin(p_best_scores)] # 群体历史最优解，np.argmin 返回最小值索引 (2,)
    
    for iteration in range(max_iterations):
        # 更新粒子速度和位置
        particles, velocities = update_particles(particles, velocities, p_best, g_best, w, c1, c2)
        # 计算新的适应度
        scores = np.apply_along_axis(objective_function, 1, particles)
        
        for i in range(num_particles):
            # 更新个体历史最优解
            if scores[i] < p_best_scores[i]:
                p_best[i] = particles[i]
                p_best_scores[i] = scores[i]
        
        # 更新群体历史最优解
        g_best = p_best[np.argmin(p_best_scores)]
        print(f"Iteration {iteration+1}/{max_iterations}, Best Score: {min(p_best_scores)}")
    
    return g_best, min(p_best_scores)

best_position, best_score = pso(num_particles, dimensions, bounds, max_iterations, w, c1, c2)
print(f"Best Position: {best_position}, Best Score: {best_score}")

在我的问题当中，粒子群优化算法的效果比前两者要慢很多，甚至有时候比暴力搜索还要慢。我们也容易看出粒子群优化算法的计算量是比较大的。

总结

这三种方法都是基于概率的优化算法。在比较复杂的优化问题中，往往比较难推导出一个可微的目标函数，以至于无法使用梯度下降法。这时候，这些启发式优化算法就显得非常有用了。

留言